This is the companion website for the paper Understanding Optimization in Deep Learning with Central Flows, published at ICLR 2025.

Understanding optimization in deep learning with central flows

Jeremy Cohen* Alex Damian*

Ameet Talwalkar J. Zico Kolter Jason D. Lee

*Alex and Jeremy contributed equally; author order determined by coin flip

A vision transformer is trained on a subset of CIFAR-10 using gradient descent. The central flow (black) accurately matches the trajectory of gradient descent.

This work takes a step towards a theory of optimization in deep learning. Traditional theories of optimization cannot describe the dynamics of optimization in deep learning, even in the simple setting of deterministic (i.e. full-batch) training. The challenge is that optimizers typically operate in a complex oscillatory regime termed the edge of stability. In this work, we develop theory that can describe the dynamics of optimization in this regime.

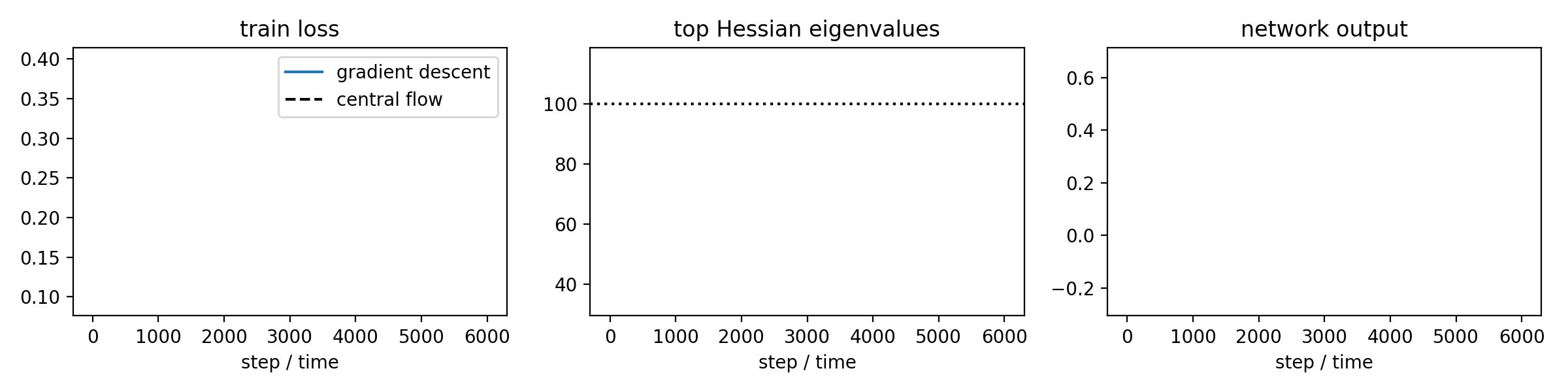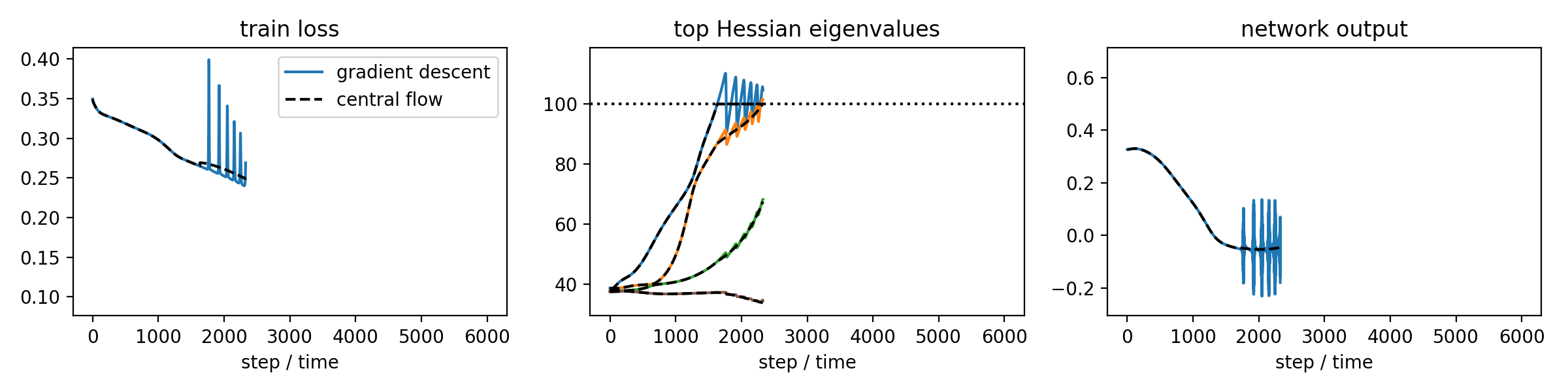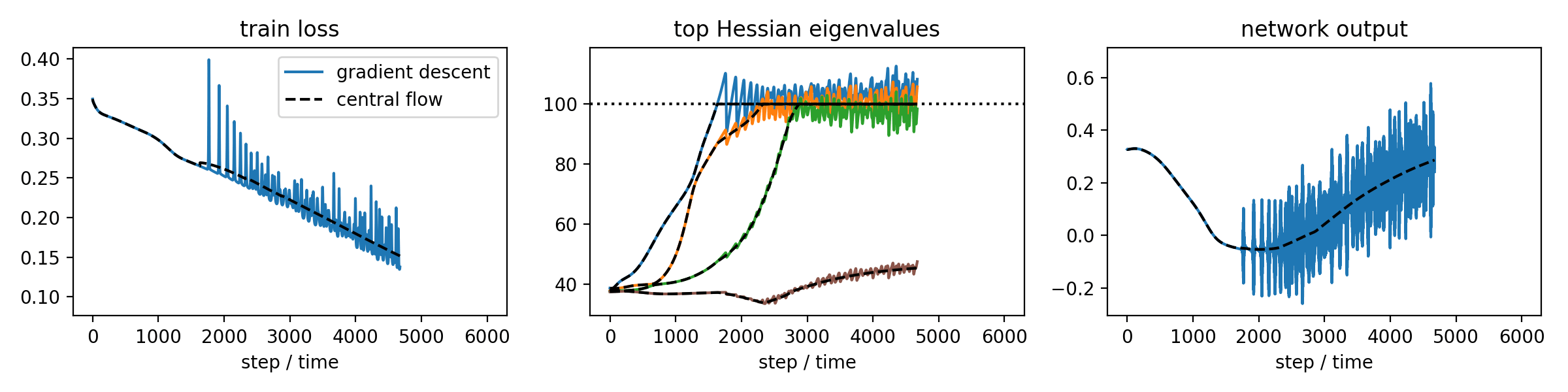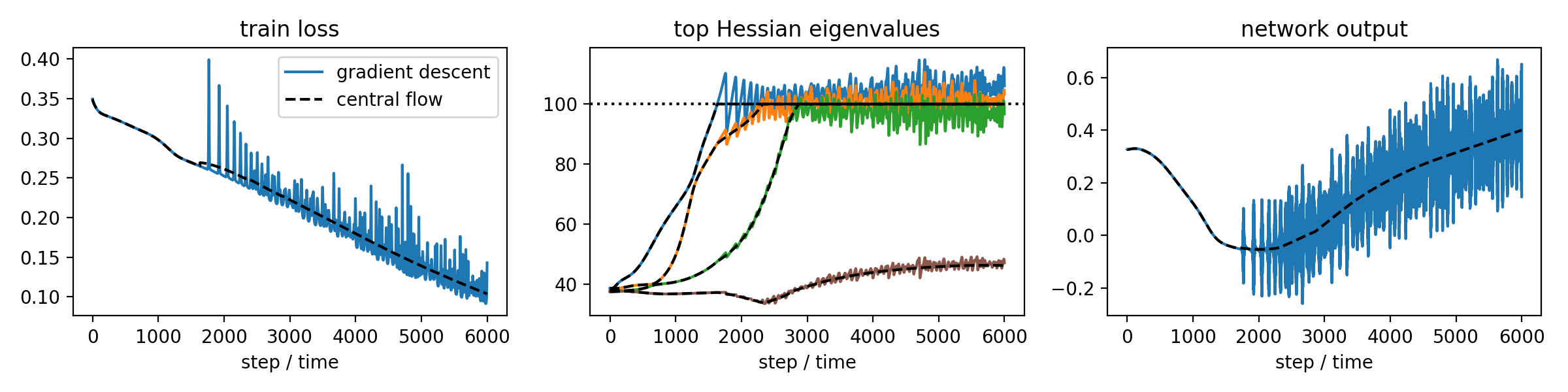
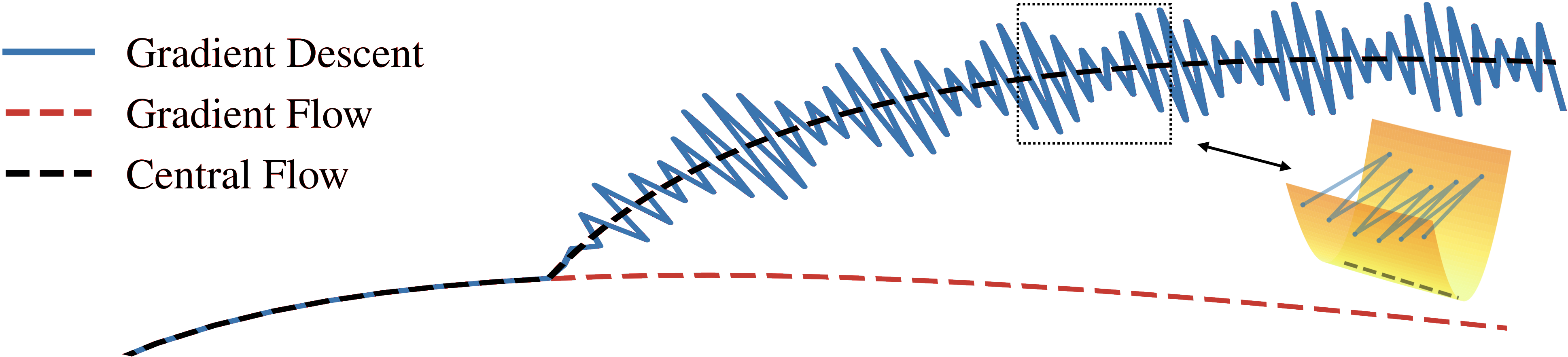
Our key insight is that while the exact dynamics of an oscillatory optimizer may be challenging to analyze, the time-averaged (i.e. locally smoothed) dynamics are often much easier to understand. We characterize these dynamics with a central flow: a differential equation that directly models the time-averaged trajectory of an oscillatory optimizer, as illustrated in the following cartoon.

In this cartoon, gradient descent (blue) takes an oscillatory path through weight space. The central flow (black) is a smooth curve that characterizes this trajectory.

This site is organized as follows, paralleling different sections of the paper:

In Part I, we analyze gradient descent, the simplest optimizer.
In Part II, we examine Scalar RMSProp, a simple adaptive optimizer.
In Part III, we study RMSProp, i.e. Adam without momentum.

Our focus is on the simple setting of deterministic (i.e. full-batch) optimization, because even this simple setting is not yet understood by existing theory. We regard our analysis of deterministic optimization as a necessary stepping stone to a future analysis of stochastic optimization.

Although our analysis is based on informal mathematical reasoning, we hold the resulting theory to the unusually high standard of rendering accurate numerical predictions about the optimization trajectories of real neural networks.

Interested in this line of work? Consider pursuing a PhD with Alex Damian, who will join the MIT Math and EECS departments in Fall 2026.